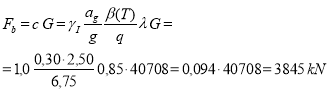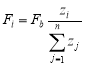Acțiunea seismică

1. Parametri de proiectare

 Acțiunea seismică de proiectare se cuantifică în acord cu prevederile codului P100-1/2013, capitolul 2 și capitolul 3, și este definită prin intermediul următorilor parametri:

a)      intervalul mediu de recurenţă (IMR) de referinţă al acţiunii seismice pentru proiectarea la Starea Limită Ultimă egal cu 225 de ani (probabilitate de depăşire de 20% în 50 de ani), stabilit conform prevederilor capitolului 2.1 din cod;

b)     accelerația orizontală a terenului pentru proiectare, a_g, egală cu 0,3g pentru București conform prevederilor capitolului 3 din cod, unde g este accelerația gravitațională aproximativ egală cu 10 m/s²

c)      perioadele de control (colţ) T_B, T_C , T_D ale spectrului de răspuns pentru componentele orizontale ale mişcării seismice pentru București stabilite conform prevederilor capitolului 3 din cod : T_C=1,60 s, T_B=0,32 s și T_D=2,00 s.

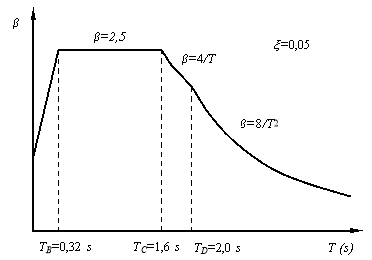
Spectrul normalizate de răspuns elastic ale acceleraţiilor absolute pentru componentele orizontale ale mişcării terenului (β)

 

 Spectrul normalizat de răspuns elastic prezentat în figură corespunde unei fracțiuni din amortizarea critică, ξ, egală cu 0,05. Această valoare este potrivită structuri în cadre de beton armat, nefiind necesară modificarea valorilor spectrale pentru a ține seama de valori diferite ale ξ. Prin multiplicarea valorilor normalizate ale accelerațiilor spectrale cu accelerația orizontală a terenului pentru proiectare, a_g=0,3g, se obține spectrul de răspuns elastic al accelerațiilor absolute pentru componentele orizontale ale mișcării terenului cu o valoare maximă de 7,5 m/s².

 

Valoarea de proiectare a forței seismice

  Întrucât structura analizată îndeplinește cerințele de regularitate specificate în P100-1/2013 (sectiunea 4.4.3), în calculul seismic se poate aplica metoda forțelor laterale statice echivalente. În această metodă acțiunea seismică este reprezentată printr-un set de forțe orizontale aplicate static. Rezultanta acestor forțe este valoarea de proiectare a forței seismice. 

 Valoarea de proiectare a forței seismice se determină conform prevederilor cap. 3, 4 și 5 din P100-1/2013:

(7)

 unde 

 γ_I,e factorul de importanță-expunere la cutremur al clădirii care se stabilește conform prevederilor capitolului 4 din P100-1/2013

 q  factorul de comportare care, pentru structura analizată, se stabilește conform prevederilor capitolului 5 din P100-1/2013

λ         factor de corecţie care ţine seama de contribuţia modului propriu
fundamental prin masa modală efectivă asociată acestuia la răspunsul seismic de ansamblu

G greutatea totală a clădirii deasupra cotei teoretice de încastrare.

 Greutatea clădirii se poate calcula, în mod aproximativ, ca suma forțelor axiale din toți stâlpii, la parter (vezi tabelul urmator). Pentru un calcul mai exact, trebuie avut totuşi în vedere faptul că nu toţi stâlpii marginali şi centrali au aceleaşi arii aferente, respectiv aceleaşi lungimi aferente de grindă. Prin urmare, valorile forţelor  axiale din stâlpii unei categorii nu vor fi aceleaşi. În calculul structural valoarea de proiectare a forţei seismice a fost determinată pe baza greutăţii calculate automat de programul de calcul şi a coeficientului seismic calculat mai jos.

 

Evaluarea simplificată a greutății structurii pe baza forțelor axiale din stâlpi

		N	Nr. stâlpilori		G
		kN	similari		kN
Stâlp de colț		1083	4
Stâlp marginal		1804	10
Stâlp central		3056	6		40708

 

 Produsul este idenficat în practica de proiectare prin denumirea de coeficient seismic. Pentru determinarea coeficientului seismic este necesar să se stabilească valorile factorilor care intră în relația de calcul (7). 

 În această fază a proiectării, perioadele de vibrație ale clădirii nu pot fi determinate prin calcul exact dar pot fi estimate folosind relaţiile simplificate date în anexa B a codului P100-1/2013. Pentru clădirea analizată perioada de vibrație în modul fundamental poate fi estimată cu relația T₁=0,1n, unde n este numărul total de niveluri situate deasupra cotei teoretice de încastrare. Pentru clădirea analizată rezultă o perioadă de vibrație în modul fundamental egală cu 0,9 s pe fiecare direcție principală. Această valoare este mai mică decât 1,6 s (T_C) și mai mare decât 0,32 s (T_B). Rezultă că poate fi utilizată la determinarea coeficientului seismic valoarea β(T)=2,50 pentru ambele direcții (vezi figura anterioară). După ce se determină valorile mai exacte ale perioadelor proprii de vibraţie prin calcul structural de ansamblu, coeficientul seismic se recalculează, daca este cazul. 

 Clădirea aparține clasei III de importanță-expunere la cutremur, făcând parte din categoria structurilor de importanță obișnuită, pentru care factorul γ_I,e este egal cu 1,0  (Tabelul 4.2 din P100-1/2013).

 Factorul de corecție care ține seama de contribuția modului fundamental prin masa modală efectivă asociată acestuia se ia egal cu 0,85 conform 4.5.3.2.2 din P100-1/2013.

 Factorul de comportare q se alege egal cu valoarea maxim admisă de 6,75, conform prevederilor de la 5.2.2.2 din P100-1/2013:

(8)

 Raportul  introduce influenţa unora dintre factorii cărora li se datorează suprarezistenţa structurii, în special a redundanţei construcţiei. Pentru structuri în cadre cu mai multe niveluri şi mai multe deschideri se ia egal cu 1,35 conform prevederilor P100-1/2013.

 Rezultă astfel un coeficient seismic de 9,4% (Tabelul 2). Valoarea de proiectare a forței seismice este:

(9)

Coeficientul seismic

γ	β	ag/g	λ	q
1	2,50	0,30	0,85	6,75	9,4%

 

Distribuția pe verticală a forței seismice

 Forța seismică de proiectare reprezintă rezultanta forțelor seismice orizontale cauzate de acțiunea seismică de proiectare. Aceste forțe seismice acționează asupra masei construcției care este distribuită. În cazuri practice de proiectare, masa distribuită a construcției se schematizează printr-un număr finit de mase amplasate, de regulă, în dreptul planșeelor. La fiecare nivel, planșeul rigid și rezistent pentru acțiuni în planul său poate asigura oscilația în fază a maselor aferente. Valorile maselor la fiecare nivel pot fi calculate pe baza forțelor care încarcă stâlpii, prin multiplicare cu numărul de stâlpi asemenea și însumare, separat, la fiecare nivel.

Schematizarea distribuției masei clădirii pe înălțime

 După schematizarea masei structurii, pentru efectuarea calculului structural este necesară distribuirea forței seismice de proiectare. Aceasta se poate face utilizând relațiile (4.4) sau (4.5) din P100-1/2013. Dacă masele structurii la fiecare nivel sunt apropiate ca valoare atunci relația (4.5) devine:

(10)

 unde: 

 F_i  forța seismică de la nivelul i

z_i distanța de la nivelul teoretic de încastrare a structurii la nivelul masei cu numarul i

n numărul total de niveluri deasupra cotei teoretice de încastrare._­

 Prin aplicarea acestei relații se pot determina forțele seismice de la fiecare nivel, F_i, așa cum se arată în Tabelul 3. Prin cumularea acestor forțe pe înălțime, ΣF_bi , pornind de la ultimul nivel în jos, se obține diagrama forțelor tăietoare de nivel (vezi figura următoare). Forța tăietoare de bază reprezentată prin suma forțelor seismice de nivel este egală cu forța seismică de proiectare.

Distribuția forței seismice pe înălțime

Nivel	he	Fi	ΣFbi
	m	kN	kN
9	3,30	769	769
8	3,30	683	1452
7	3,30	598	2050
6	3,30	513	2563
5	3,30	427	2990
4	3,30	342	3332
3	3,30	256	3588
2	3,30	171	3759
1	3,30	85	3845
Fb		3845 kN

 

  

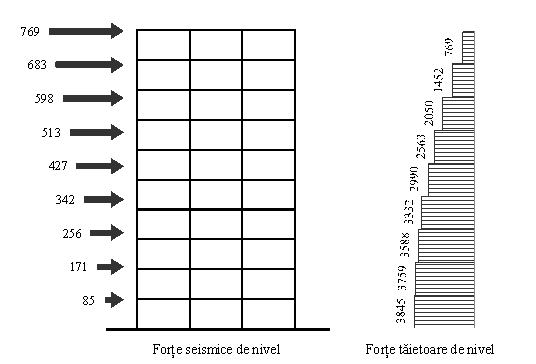
Distribuția forțelor seismice pe înălțime(kN)

Efectele torsiunii accidentale

 Torsiunea de ansamblu din cauze accidentale se cuantifică prin intermediul momentului de torsiune accidentală, calculat la fiecare nivel ca produsul dintre forța seismică de nivel și excentricitatea accidentală. Momentul de torsiune accidentală acționează structura la nivelul planșeelor având vectorul orientat în direcția verticală, Z. 

 Conform P100-1/2013, excentricitatea accidentală, e_ai, se ia egală cu 5% din lungimea laturii clădirii pe care forța seismică este perpendiculară, L_i, și se raportează la poziția calculată a centrului maselor de la fiecare nivel. 

(11)

 De exemplu, pentru ultimul nivel (9), momentul de torsiune accidentală corespunzător situației în care forța seismică acționează în direcție transversală (Y), este:

(12)

 În mod similar se determină momentele M_ti pentru fiecare nivel i și fiecare direcție de acțiune a forței seismice.

Momente de torsiune accidentală

Nivel	Fbi	Lix	eix	Mti (Fb pe dir. Y)		Liy	eiy	Mti (Fb pe dir. X)
	kN	m	m	kNm		m	m	kNm
9	769	22,7	1,14	873		16,7	0,84	642
8	683	22,7	1,14	776		16,7	0,84	571
7	598	22,7	1,14	679		16,7	0,84	499
6	513	22,7	1,14	582		16,7	0,84	428
5	427	22,7	1,14	485		16,7	0,84	357
4	342	22,7	1,14	388		16,7	0,84	285
3	256	22,7	1,14	291		16,7	0,84	214
2	171	22,7	1,14	194		16,7	0,84	143
1	85	22,7	1,14	97		16,7	0,84	71